我实验室在量子信息基础理论研究中取得重要进展：李传锋、项国勇研究组与华沙大学Alexander Streltsov等人合作，对复数这种量子资源进行了深入的研究，并取得一系列重要的进展，相关结果以“Editors’ Suggestion”（编辑推荐文章）的形式于3月1日在国际著名物理期刊《Physical Review Letters》和《Physical Review A》上联合发表。

复数是一种数学工具，然而它广泛应用于力学、电动力学和光学等物理学相关的领域中，使相应的理论有了一个优雅简洁的表述。量子力学的诞生给出了波和粒子的统一图景，进一步加强了复数在物理学中的突出作用。复数结构是否是量子力学所必须的？这个问题长期以来引起了物理学家们的争论。

项国勇等人将复数作为一种量子资源，揭示了其在局部量子态区分中有着不可替代的作用，并且更进一步在量子资源理论的框架下，研究了该种资源的度量方式以及在各种量子操作下的转化问题。他们从理论上完全解决了复数大小的鲁棒性度量问题、单比特量子态在自由操作下的转化问题以及任意纯态的在自由操作下的相互转化概率问题。项国勇等人利用参量下转换制备的双光子纠缠态，进一步测定并比较了当仅用实数测量基和可使用任意测量基情形下的局部量子态区分的成功概率，成功观察到了当使用复数测量基时其成功概率的增加，从而验证了复数在量子力学中具有重要的作用。

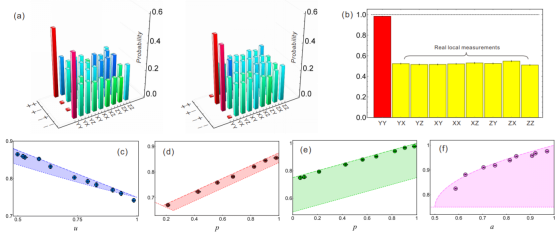
局部量子态区分成功概率的实验测定值

该工作证明了虚部在量子力学理论中是不可或缺的。审稿人认为：“I find that the quantum imaginarity can be considered as a stronger form of quantum coherence, ……., I also think that the results in the manuscript will stimulate the research on the quantum foundation and the quantum resource theories with a richer structure.（我认为量子虚部可以看成是量子相干性的一种更强的形式，……，我也认为该工作可以激发更多的量子力学基本问题和更丰富结构的量子资源理论。）”

两篇论文的第一作者为中科院量子信息重点实验室的博士后吴康达，通讯作者为项国勇教授以及华沙大学的Alexander Streltsov博士。该工作得到了科技部、国家基金委、中科院、安徽省、学校国际合作交流部以及波兰科学基金会的支持。

论文链接：

https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.126.090401

https://journals.aps.org/pra/abstract/10.1103/PhysRevA.103.032401

（中科院量子信息重点实验室、中科院量子信息和量子科技创新研究院、科研部）

编辑时间：2021-03-04 08:27:33